gams入门教程

科学软件网提供的软件上千款，涉及所有学科领域，您所需的软件，我们都能提供。科学软件网提供的软件涵盖领域包括经管，仿真，地球地理，生物化学，工程科学，排版及网络管理等。同时，还提供培训、课程（包含34款软件，66门课程）、实验室解决方案和项目咨询等服务。
Equation Declaration
Equations must be declared and defined in separate statements. The format of the declaration is the same as for other GAMS
entities. First comes the keyword, Equations in this case, followed by the name, domain and text of one or more groups of
equations or inequalities being declared. Our transportation model contains the following equation declaration:
Equations
cost define objective function
supply(i) observe supply limit at plant i
demand(j) satisfy demand at market j ;
Keep in mind that the word Equation has a broad meaning in GAMS. It encompasses both equality and inequality
relationships, and a GAMS equation with a single name can refer to one or several of these relationships. For example, cost
has no domain so it is a single equation, but supply refers to a set of inequalities defined over the domain i.

通用代数建模系统（GAMS）是数学编程和优化的建模系统。它由一个语言编译器和一个稳定的集成各种高性能的求解器组成。GAMS适用于复杂的、大规模的建模应用，并允许您创建大的维护模型以很快的适应新的情况。


立的模型和求解器
提供**过25个广泛和多样化的求解器组合，包括所有预期的商业化求解器。
LP/MIP/QCP/MIQCP: CPLEX, GUROBI, MOSEK, XPRESS
NLP: CONOPT, IPOPTH, KNITRO, MINOS, SNOPT
MINLP: ALPHAECP, ANTIGONE, BARON, DICOPT, OQNLP, SBB
混合互补问题求解器（MCP）、平衡约束数学规划求解器(MPEC)和约束非线性系统求解器(CNS)
免费到每个GAMS系统中的 (比如 BONMIN (MINLP), CBC (LP, MIP), COUENNE (MINLP), IPOPT (NLP)。教育版还包括了SCIP和SOPLEX。
选择使用的求解器非常简单---只要改变一行代码或者调整一个选项设置就可以了。想要比较求解器的性能或者看有什么改进的可能，也不需要做任何的设置。同样的，模型类型可以轻松切换（比如：线性和非线性），尝试不同的公式也非常的*。通过使用GAMS，您可以得到一个广泛类型的模型和求解器的环境。


立的模型和数据
你可以编写立的模型数据，包括各种不同来源的数据，从ASCII到Excel或者Access 以及其他各种来源。比如使用GDX（GAMS数据交换）文件格式。GDX文件可以保存一个或多个GAMS符号的值，比如集、参数变量和方程。GDX文件可以为GAMS模型准备数据、展示GAMS模型的结果、使用不同的参数为这同一个模型保存结果等。GDX文件不能保存一个模型的公式或者执行语句。GDX文件二进制文件，可在不同平台进行移植。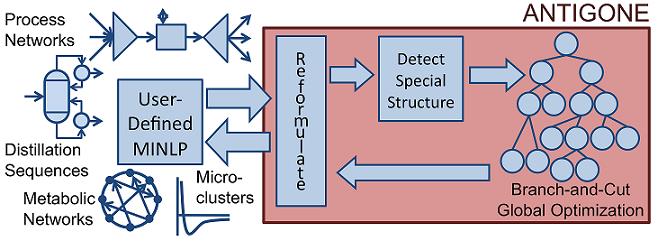

A GAMS Tutorial by Richard E. Rosenthal
1 Introduction
The introductory part of this book ends with a detailed example of the use of GAMS for formulating, solving, and analyzing
a small and simple optimization problem. Richard E. Rosenthal of the Naval Postgraduate School in Monterey, California
wrote it. The example is a quick but complete overview of GAMS and its features. Many references are made to other parts
of the book, but they are only to tell you where to look for more details; the material here can be read profitably without
reference to the rest of the book.
The example is an instance of the transportation problem of linear programming, which has historically served as a 'laboratory
animal' in the development of optimization technology. [See, for example, Dantzig (1963) 1. ] It is a good choice for
illustrating the power of algebraic modeling languages like GAMS because the transportation problem, no matter how large
the instance at hand, possesses a simple, exploitable algebraic structure. You will see that almost all of the statements in the
GAMS input file we are about to present would remain unchanged if a much larger transportation problem were considered.
In the familiar transportation problem, we are given the supplies at several plants and the demands at several markets for a
single commodity, and we are given the unit costs of shipping the commodity from plants to markets. The economic question
is: how much shipment should there be between each plant and each market so as to minimize total transport cost?
The algebraic representation of this problem is usually presented in a format similar to the following

Variables
The decision variables (or endogenous variables ) of a GAMS-expressed model must be declared with a Variables statement.
Each variable is given a name, a domain if appropriate, and (optionally) text. The transportation model contains the following
example of a Variables statement.
Variables
x(i,j) shipment quantities in cases
z total transportation costs in thousands of dollars ;
This statement results in the declaration of a shipment variable for each (i,j) pair. (You will see in Chapter Equations, how
GAMS can handle the typical real-world situation in which only a subset of the (i,j) pairs is allowable for shipment.)
The z variable is declared without a domain because it is a scalar quantity. Every GAMS optimization model must contain
one such variable to serve as the quantity to be minimized or maximized.
Once declared, every variable must be assigned a type. The permissible types are given in table Table 3.
Table 3 : Permissible variable types
科学软件网为全国大多数高校提供过产品或服务，销售和售后团队，确保您售后**！
http://turntech8843.b2b168.com