gams程序_正版软件

科学软件网专注提供科研软件。截止目前，共代理千余款，软件涵盖各个学科。除了软件，科学软件网还提供课程，包含34款软件，66门课程。热门软件有：spss，stata，gams，sas，minitab，matlab，mathematica，lingo，hydrus，gms，pscad，mplus，tableau，eviews，nvivo，gtap，sequncher，simca等等。
Here are some points to remember when using the list format.
1. The list of domain elements and their respective parameter values can be laid out in almost any way you like. The only
rules are that the entire list must be enclosed in slashes and that the element-value pairs must be separated by commas
or entered on separate lines.
2. There is no semicolon separating the element-value list from the name, domain, and text that precede it. This is because
the same statement is being used for declaration and assignment when you use the list format. (An element-value list
by itself is not interpretable by GAMS and will result in an error message.)
3. The GAMS compiler has an unusual feature called domain checking, which verifies that each domain element in the
list is in fact a member of the appropriate set. For example, if you were to spell 'Seattle' correctly in the statement
declaring Set i but misspell it as 'Seatle' in a subsequent element-value list, the GAMS compiler would give you an
error message that the element 'Seatle' does not belong to the set i.
4. Zero is the default value for all parameters. Therefore, you only need to include the nonzero entries in the element-value
list, and these can be entered in any order .

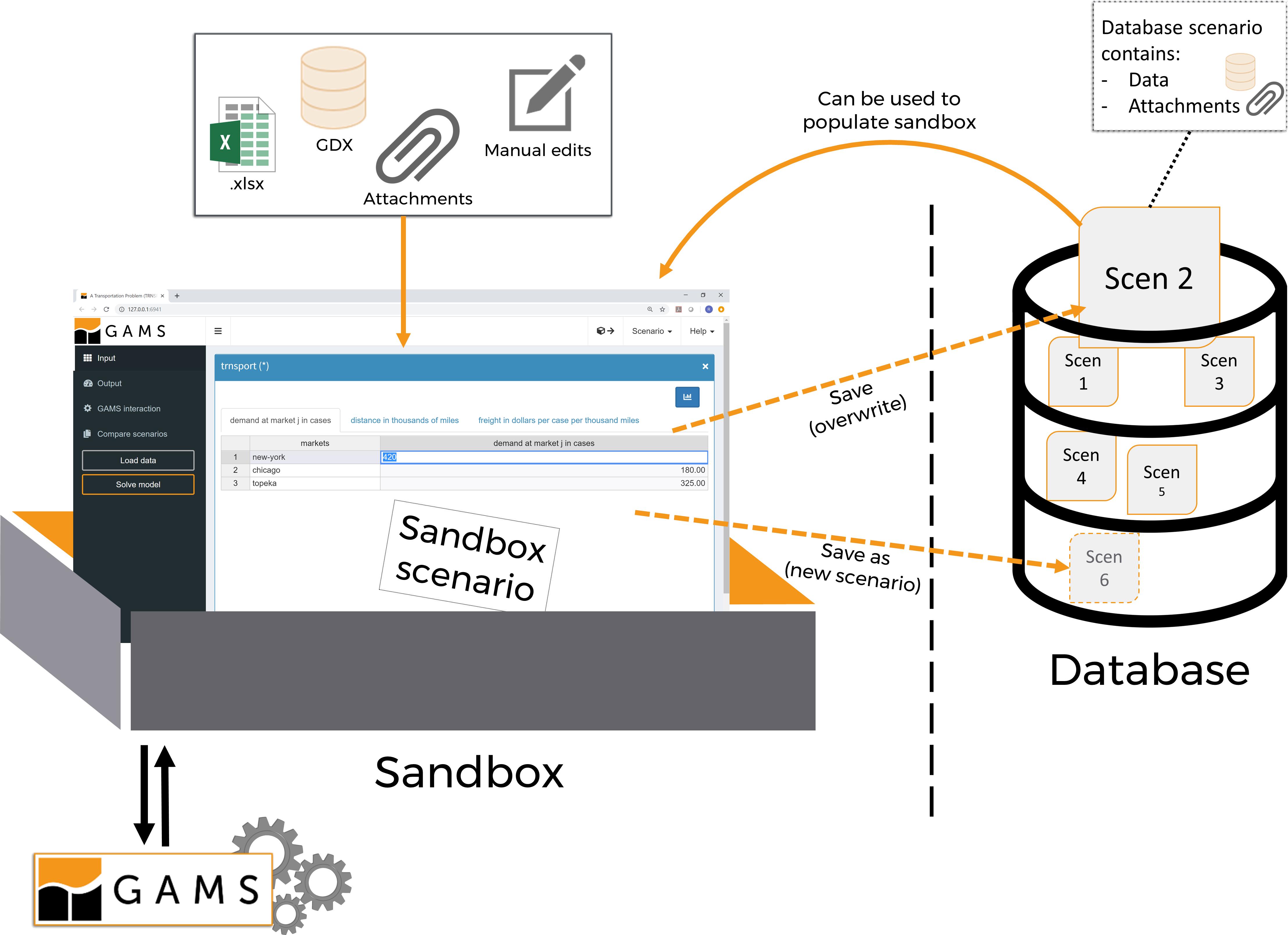
A GAMS Tutorial by Richard E. Rosenthal
1 Introduction
The introductory part of this book ends with a detailed example of the use of GAMS for formulating, solving, and analyzing
a small and simple optimization problem. Richard E. Rosenthal of the Naval Postgraduate School in Monterey, California
wrote it. The example is a quick but complete overview of GAMS and its features. Many references are made to other parts
of the book, but they are only to tell you where to look for more details; the material here can be read profitably without
reference to the rest of the book.
The example is an instance of the transportation problem of linear programming, which has historically served as a 'laboratory
animal' in the development of optimization technology. [See, for example, Dantzig (1963) 1. ] It is a good choice for
illustrating the power of algebraic modeling languages like GAMS because the transportation problem, no matter how large
the instance at hand, possesses a simple, exploitable algebraic structure. You will see that almost all of the statements in the
GAMS input file we are about to present would remain unchanged if a much larger transportation problem were considered.
In the familiar transportation problem, we are given the supplies at several plants and the demands at several markets for a
single commodity, and we are given the unit costs of shipping the commodity from plants to markets. The economic question
is: how much shipment should there be between each plant and each market so as to minimize total transport cost?
The algebraic representation of this problem is usually presented in a format similar to the following

It is important to emphasize the presence of the semicolon at the end of the first line. Without it, the GAMS compiler would
attempt to interpret both lines as parts of the same statement. (GAMS would fail to discern a valid interpretation, so it would
send you a terse but helpful error message.)
The effects of the first statement above are to declare the parameter c, to specify the domain (i,j), and to provide some
documentary text. The second statement assigns to c(i,j) the product of the values of the parameters f and d(i,j).
Naturally, this is legal in GAMS only if you have already assigned values to f and d(i,j) in previous statements.
The direct assignment above applies to all (i,j) pairs in the domain of c. If you wish to make assignments for specific
elements in the domain, you enclose the element names in quotes. For example,

Objective Function
This is  a reminder that GAMS has no explicit entity called the objective function. To specify the function to be optimized,
you must create a variable, which is free (unconstrained in sign) and scalar-valued (has no domain) and which appears in an
equation definition that equates it to the objective function.
科学软件网不定期举办各类公益培训和讲座，让您有更多机会免费学习和熟悉软件。
http://turntech8843.b2b168.com